2.1.1.10.1. Общие сведения системы привода вспомогательных агрегатов мотора

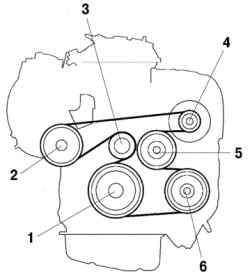
Рис. 2.36. Привод агрегатов вспомогательного оборудования: 1 – шкив коленчатого вала; 2 – шкив насоса усилителя рулевого управления; 3 – натяжной шкив автоматического механизма натяжения; 4 – шкив генератора переменного тока; 5 – шкив насоса охлаждающей ж

Привод агрегатов вспомогательного оборудования двигателя осуществляется одним многоручьевым ремнем. Вспомогательные агрегаты двигателя приводятся в действие одним многоручьевым ремнем. Это уменьшает общую длину, массу и количество деталей двигателя. Автоматический механизм натяжения устраняет потребность в регулировке натяжения ремня.